卷积神经网络概述

计算机视觉

• 计算机视觉的成果可以应用到其他领域（如：语音识别）

• 两个作用

  1. 识别

     

  2. 检测

     

• 图像的数据量非常大，所以需要使用卷积计算来进行处理，而不是全连接

边缘检测示例

• 神经网络的前几层是如何检测边缘的，后面的层有可能检测到物体的部分区域，更靠后的一些层可能检测到完整的物体（如：人脸）

  

• 构造一个用于检测垂直边缘的过滤器（filter，或核），如：$\begin{bmatrix} 1&0&-1\\1&0&-1\\1&0&-1 \end{bmatrix}$

• 进行卷积计算，得：

  

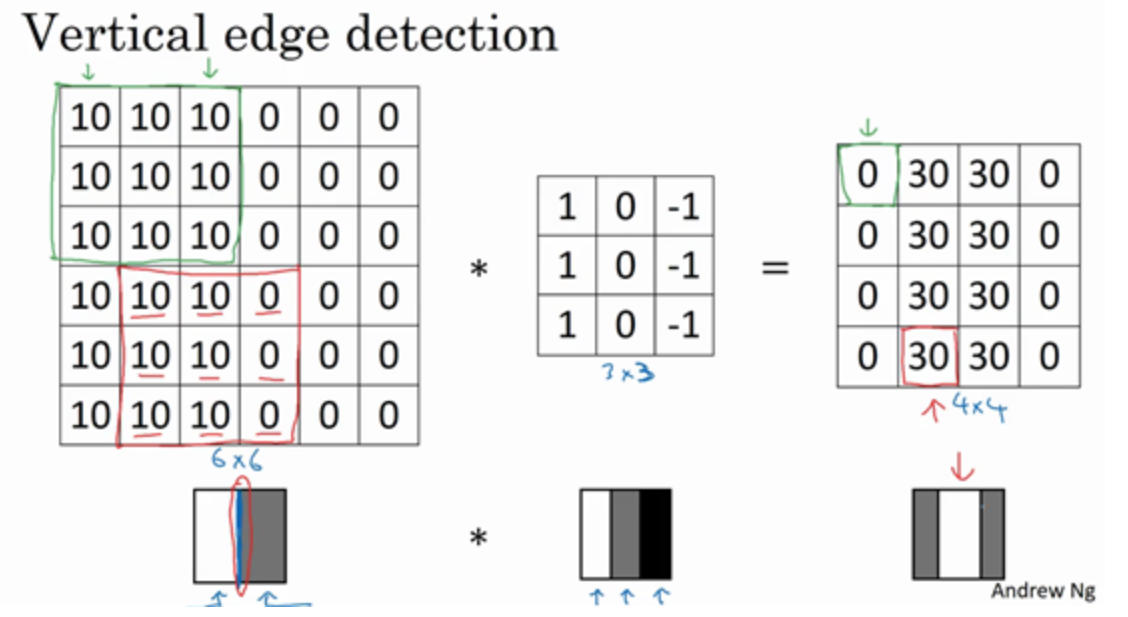
  中间一段亮一点的区域对应到这个6×6图像中间的垂直边缘；这里得到的边缘较宽是因为原图像太小，只有6×6；这个卷积核的意义是如果左边亮右边暗，就视为一个边缘；

更多边缘检测内容

• 将上面的图像翻转，检测到的是负边（由暗到亮）

  

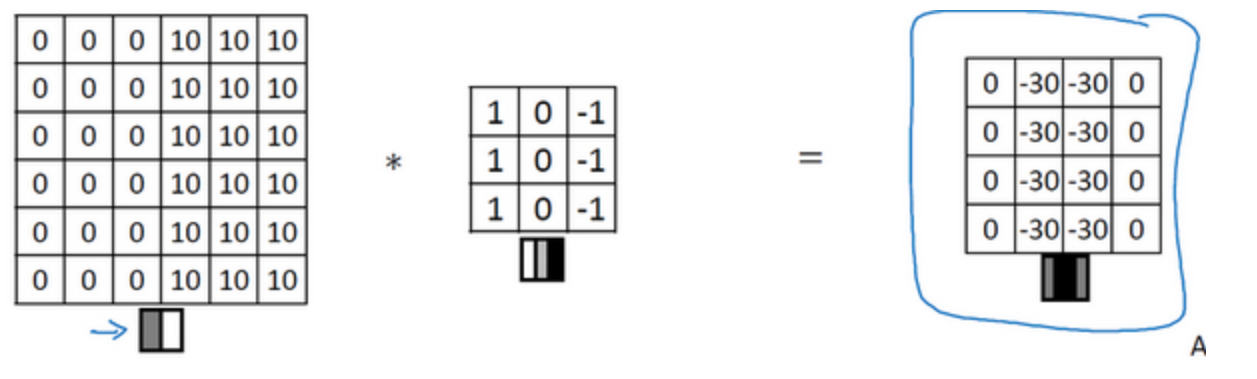
• 可以推出检测水平边缘的过滤器：$\begin{bmatrix} 1&1&1\\0&0&0\\-1&-1&-1\end{bmatrix}$

• 考虑一个更复杂的例子，左边有一个水平正边缘，右边有一个水平负边缘，里面的10和-10是因为对应过滤器所在的位置有正有负抵消了一部分，当原图像很大时，抵消的部分相对就很小了

  

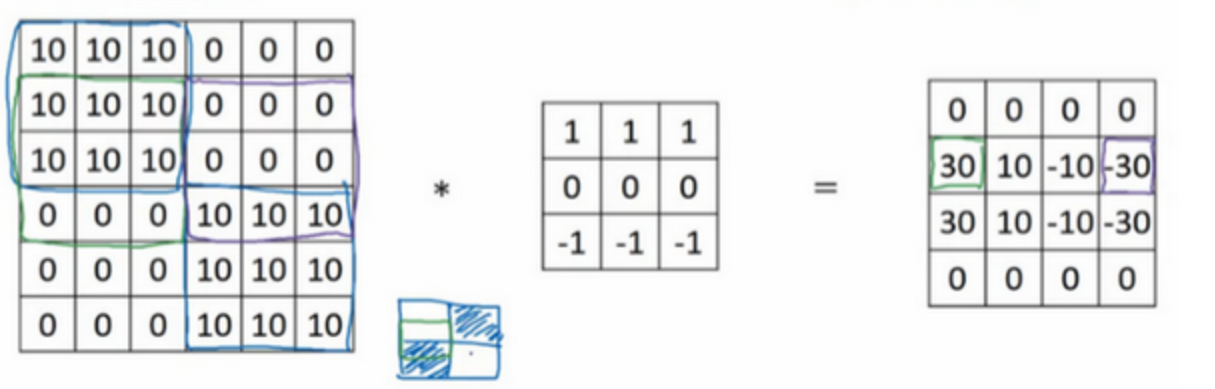
• 实际中有很多的过滤器用于检测边缘，但通常做法是将过滤器设置成参数，通过反向传播找到最适合的过滤器，甚至检出任何角度的边缘

Padding

• 对于一个$n×n$的图像，用一个$f×f$的过滤器进行卷积，输出维度是$(n-f+1)×(n-f+1)$，有两个缺点

  1. 多次卷积后图像会变得特别小
  2. 角落边缘的像素只被一个输出所触碰或者使用，丢掉了图像边缘位置的许多信息

• 使用padding，输出维度是$(n+2p-f+1)×(n+2p-f+1)$

  

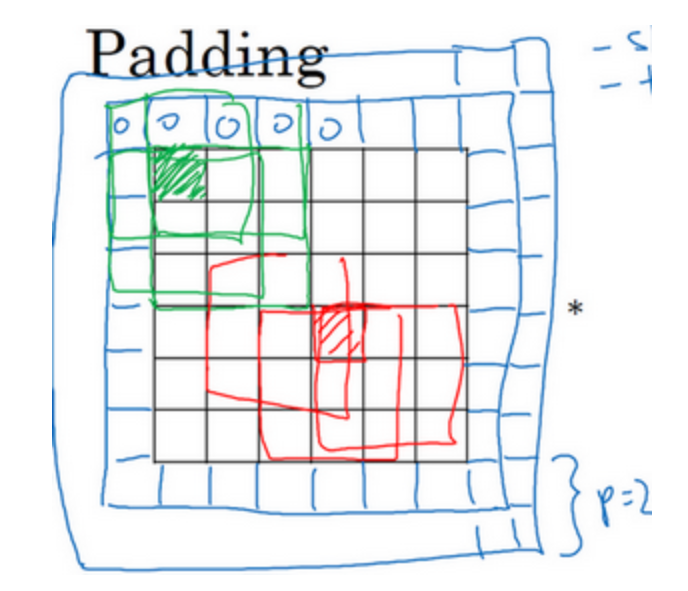
• 两种卷积方式：

  1. valid：不填充
  2. same：输出大小和输入大小一样

• 计算机视觉中，$f$通常是奇数

  1. 如果$f$是一个偶数，会产生不对称填充
  2. $f$是奇数会有一个中心点，便于指出过滤器的位置

Stride

• 步长的值是卷积核每次移动的距离
• 输出维度是$\lfloor\frac{n+2p-f}{s}+1\rfloor$（向下取整）
• 在数学领域中，卷积前要对卷积核进行翻转操作，但在深度学习领域中不需要，约定俗成

三维卷积

• $h×w×c$；注意$c$是相等的，输出的层数变成了1；27个数相加

  

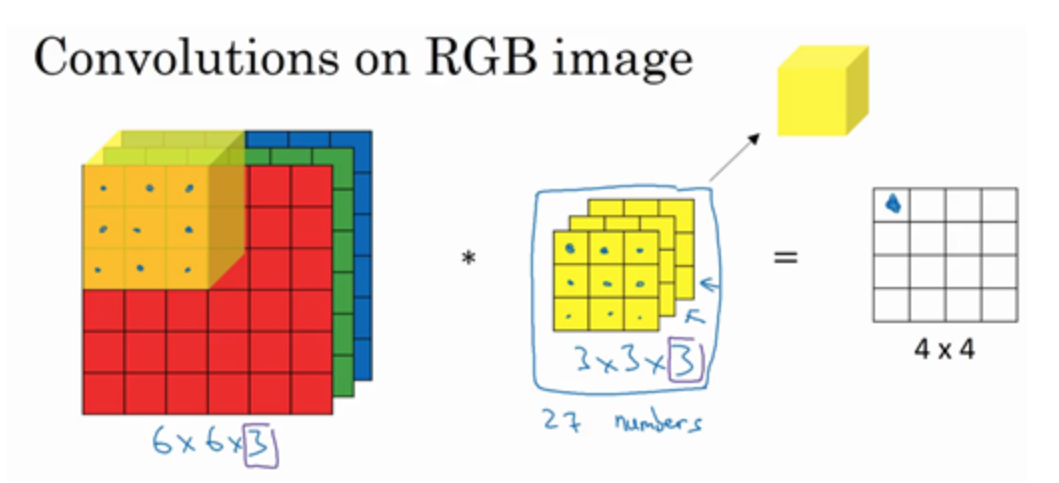
• 如果想检测图像红色通道的边缘，过滤器设置为$\begin{bmatrix} 1&0&-1\\1&0&-1\\1&0&-1 \end{bmatrix}$ $\begin{bmatrix} 0&0&0\\0&0&0\\0&0&0 \end{bmatrix}$ $\begin{bmatrix} 0&0&0\\0&0&0\\0&0&0 \end{bmatrix}$;如果不关心垂直边界在哪个颜色通道，过滤器设置为$\begin{bmatrix} 1&0&-1\\1&0&-1\\1&0&-1 \end{bmatrix}$ $\begin{bmatrix} 1&0&-1\\1&0&-1\\1&0&-1 \end{bmatrix}$ $\begin{bmatrix} 1&0&-1\\1&0&-1\\1&0&-1 \end{bmatrix}$，参数的选择不同，可以得到不同的特征检测器

• 如果同时使用多个过滤器，输出的第三个维度是过滤器的个数，这里的2的来源于使用了两个不同的过滤器，即输出的通道数等于你要检测的特征数

  

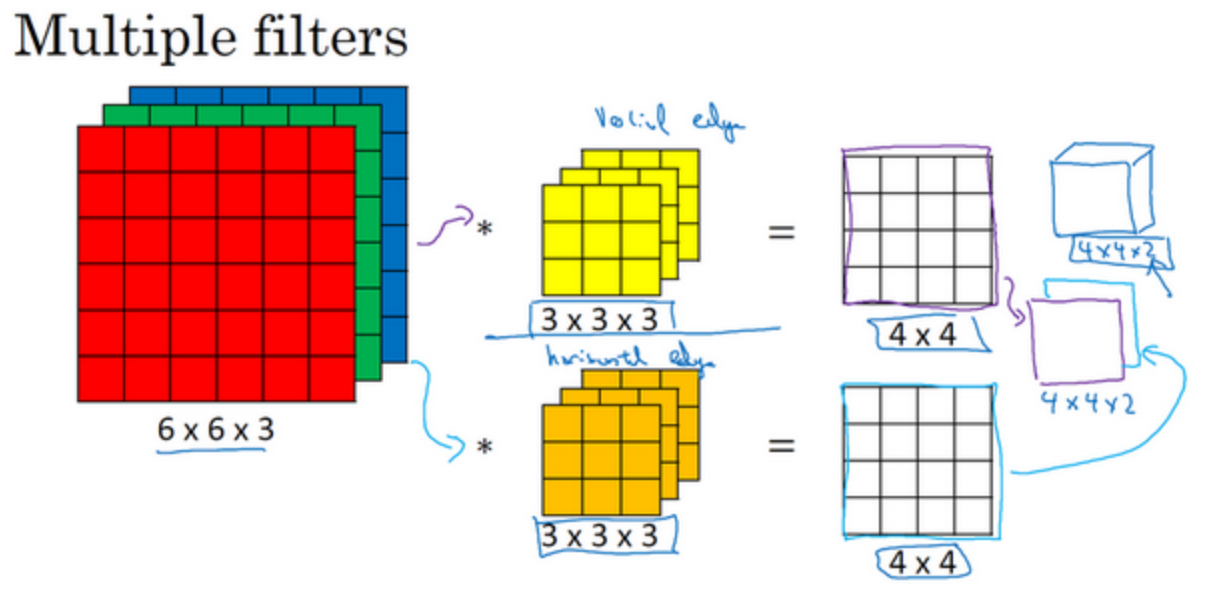
单层卷积网络

• 构造一个卷积层：

  过滤器用变量$W^{[1]}$表示，实际上是一个线性函数；

  输入是$a^{[0]}$；

  $b^{[1]}$是偏差（bias），16个元素都要加上；

  $a$是当前层的输出，也是下一层的输入；

  $g()$是一个非线性激活函数ReLU，得到的4×4×2矩阵，成为神经网络的下一层，也就是激活层

  $a^{[1]}=g(W^{[1]}a^{[0]}+b^{[1]})$

  

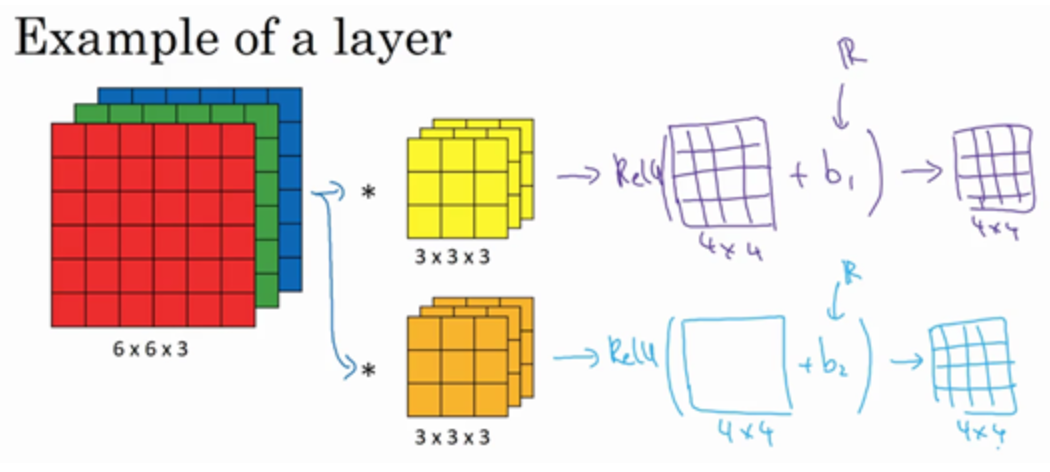
• 不论输入图片有多大，参数始终不变。可以“避免过拟合”

• 激活函数：

简单卷积网络示例

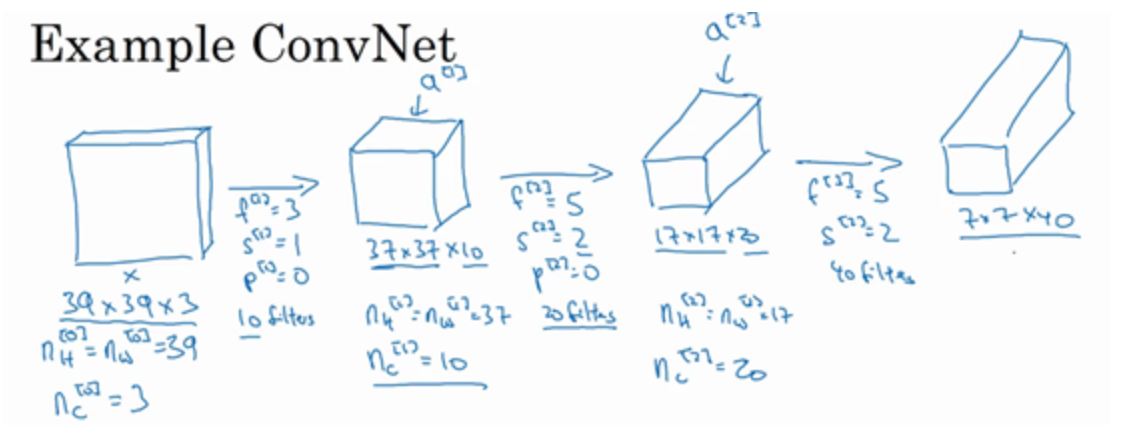
将得到的一组7×7×40的特征扁平化为一个向量，输出到softmax/logistic层

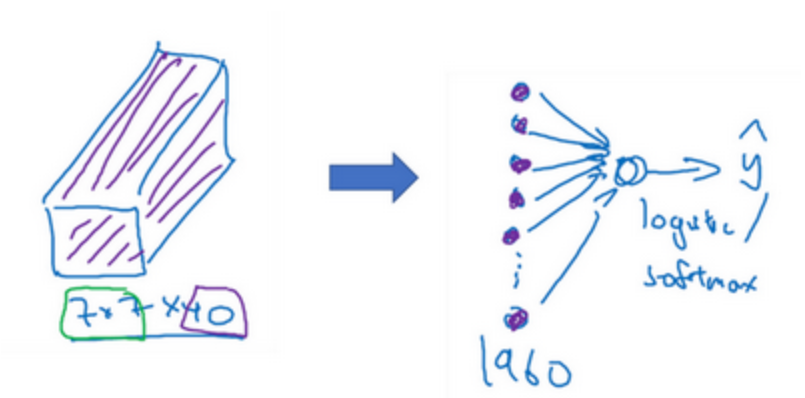
Pooling Layer

• 作用：缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性

• 计算方式：两个参数——s : stride 和 f : size of filter

  1. max pooling：把4×4的输入拆分成不同的区域，输出的每个元素都是其对应颜色区域中的最大元素值

     

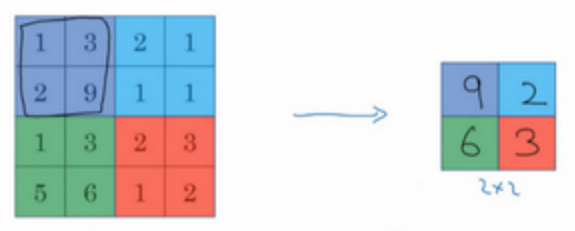
     把这个4×4输入看作是某些特征的集合，数字大意味着可能探测到了某些特定的特征，最大化操作的功能就是只要在任何一个象限内提取到某个特征，它都会保留在最大化的池化输出里；有一组超参数（f和s），但并没有参数需要学习；如果输入是三维的，那么输出也是三维的；最大池化很少用padding

     

  2. average pooling：不常用，选取的是平均值

     

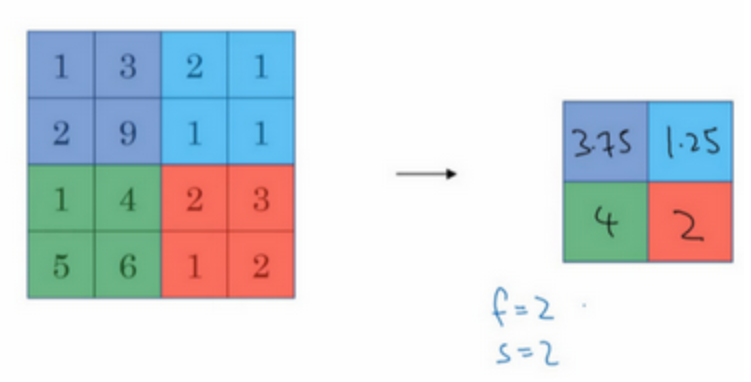
卷积神经网络示例

• 下面是一个经典的手写数字识别的CNN，Layer1和Layer2分别由一层卷积和一层池化组成，将得到的5×5×16扁平化为一个400维的特征向量，FC3和FC4分别是两个全连接层，最后将结果放入softmax层输出10个结果之一

  

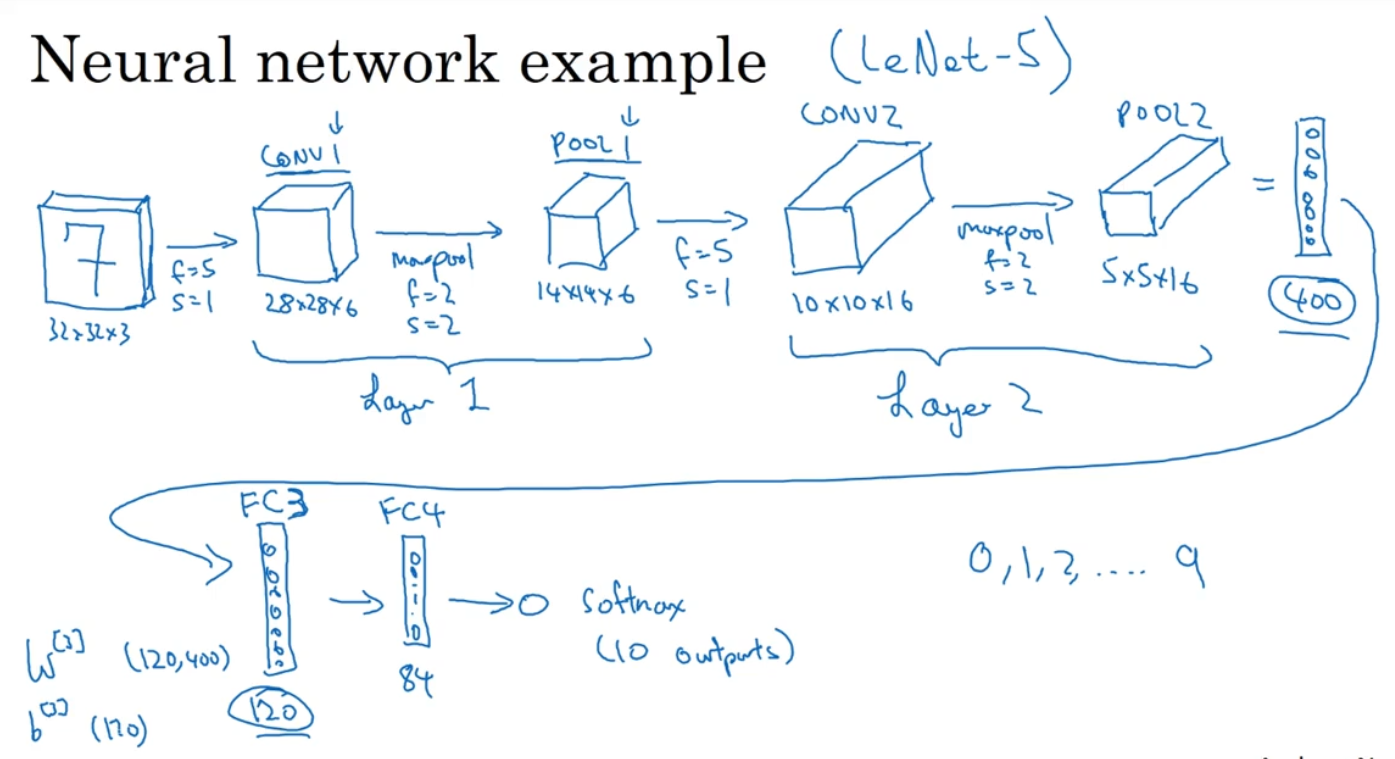
• 一种写法是一层卷积+一层池化=一层，另一种是一层卷积或一层池化都算是一层，前者的原因是池化层没有权重和参数，只有一些提前设定好的超参数，所以不认为是一层；全连接层就是一个基础的神经网络层，在120×400的维度上有一个权重矩阵，两边的每一个参数都相互连接；另一种模式是一个或多个卷积层后面跟着一个池化层，然后跟着一个全连接层

• 第一，池化层和最大池化层没有参数；第二卷积层的参数相对较少；第三，随着神经网络的加深，激活值尺寸会逐渐变小，如果激活值尺寸下降太快，也会影响神经网络性能

  

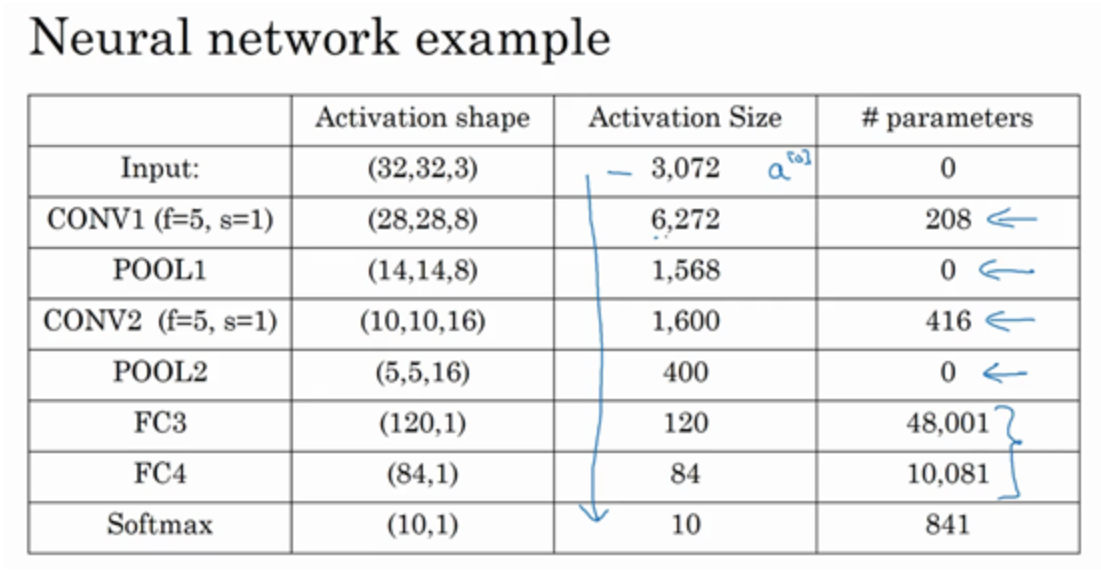
为什么使用卷积

• 举个例子：6个大小为5×5的过滤器，输出维度为28×28×6。32×32×3=3072，28×28×6=4704，构建一个传统神经网络，其中一层含有3072个单元，下一层含有4074个单元，两层中的每个神经元彼此相连，权重矩阵的参数有4074×3072≈1400万，而如果使用卷积连接，每个过滤器都是5×5，一个过滤器有25个参数，再加上偏差参数，那么每个过滤器就有26个参数，一共有6个过滤器，所以参数共计156个，参数的数量大大减少

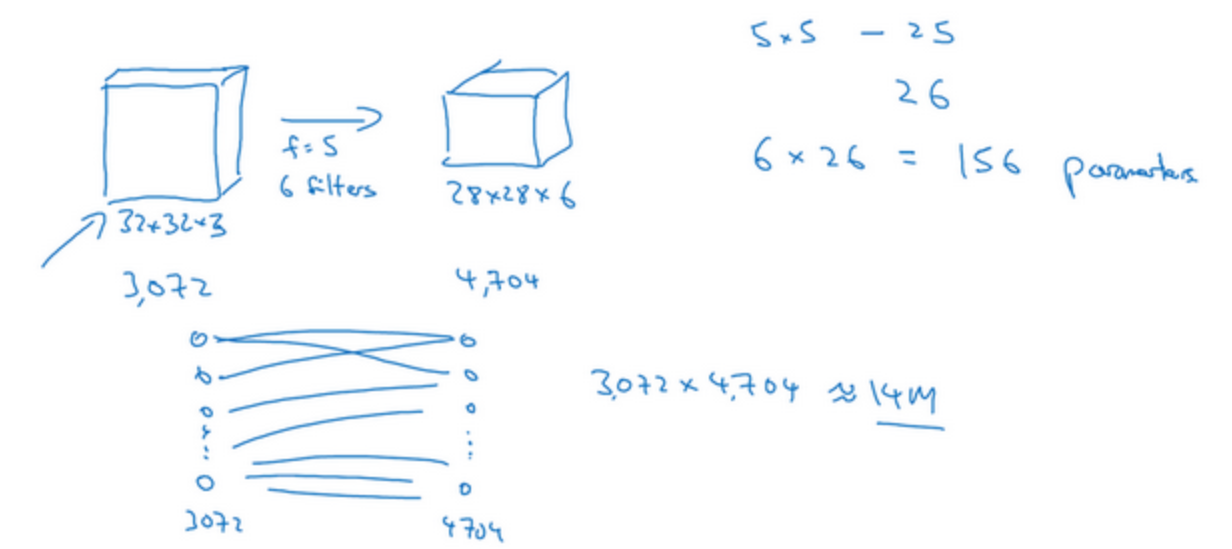
• 原因：

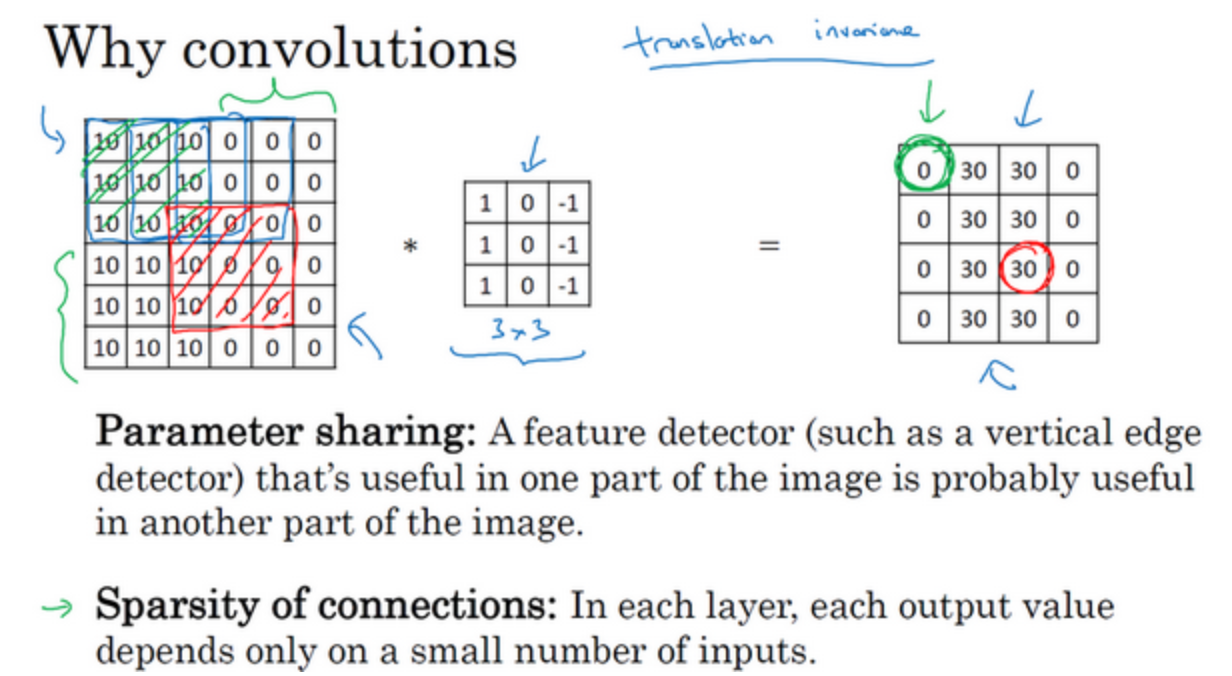
  1. 参数共享：特征检测如垂直边缘检测如果适用于图片的某个区域，那么它也可能适用于图片的其他区域，它不仅适用于边缘特征这样的低阶特征，同样适用于高阶特征，例如提取脸上的眼睛，猫或者其他特征对象（边缘检测是基础），
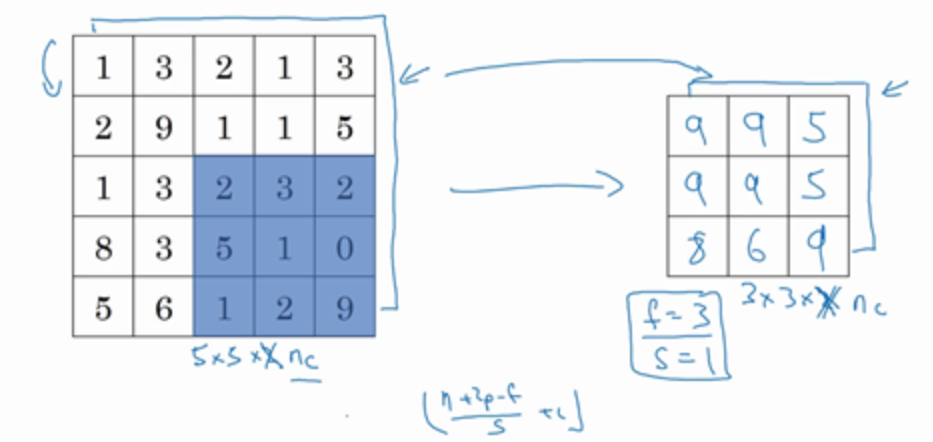
  2. 稀疏连接：后面卷积层中的0是通过3×3的卷积计算得到的，它只依赖于这个3×3的输入的单元格，右边这个输出单元（元素0）仅与36个输入特征中9个相连接。而且其它像素值都不会对输出产生任何影响
  

• 神经网络可以通过这两种机制减少参数，以便我们用更小的训练集来训练它，从而预防过度拟合。卷积神经网络善于捕捉平移不变。神经网络的卷积结构使得即使图片移动几个像素，这张图片依然具有非常相似的特征，应该属于同样的输出标记，使网络更加健壮

---

• ← Previous Post
• Next Post →